Qu'est-ce qu'un Contrôleur PID ?

---

Un contrôleur PID (Proportionnel, Intégral, Dérivé) est utilisé pour ajuster dynamiquement un système afin de minimiser une erreur entre une valeur mesurée et une consigne désirée.

Ce type de contrôleur est largement employé dans de nombreux domaines, tels que la robotique, le contrôle moteur, l'équilibrage, les drones, les systèmes de chauffage/climatisation et bien d'autres applications industrielles.

Saviez-vous ?

Le contrôleur PID a été inventé en 1911 par Elmer Sperry pour le pilotage automatique des navires, et a été formalisé mathématiquement en 1922 par Nicolas Minorsky.

Principe Général du PID

e(t) = consigne - mesure

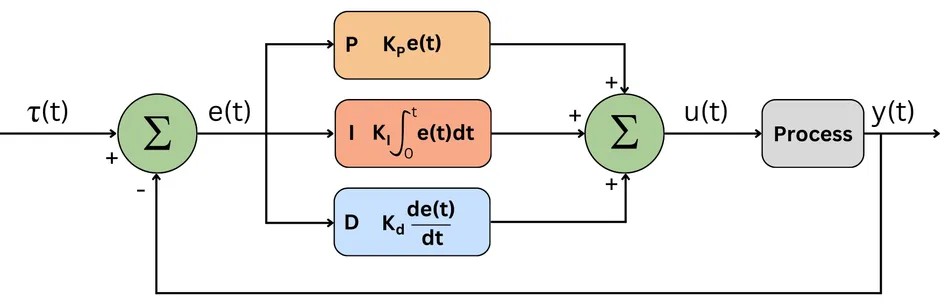
Schéma de fonctionnement d'un contrôleur PID

Équation Mathématique du PID

$$u(t) = K_p \cdot e(t) + K_i \int e(t) dt + K_d \cdot \frac{de(t)}{dt}$$

Un contrôleur PID agit en combinant trois termes, chacun ayant un rôle spécifique dans la régulation du système :

• Proportionnel (P) : Il génère une action proportionnelle à l'erreur actuelle. Un grand coefficient Kp entraîne une correction rapide mais peut causer une instabilité.


• Intégral (I) : Il corrige l’erreur accumulée dans le temps pour éliminer l’écart statique. Un Ki trop grand peut rendre le système lent et provoquer des oscillations.


• Dérivé (D) : Il anticipe les variations de l'erreur en utilisant sa dérivée. Il aide à réduire les oscillations mais est sensible aux bruits du signal.

Comment appliquer cette notion au projet ?

Nous nous appuierons principalement sur les travaux de Nick Mosher, qui propose une approche détaillée pour l'implémentation du contrôleur PID dans un environnement de programmation. Nous examinerons comment adapter ses principes à notre robot bipède et comment optimiser son utilisation afin d'assurer une régulation précise et efficace des mouvements et de la stabilisation.

#include <iostream>
#include <chrono>
#include <functional>

template <class T>
class PIDController {
private:
    double _p, _i, _d;
    T target, output, currentFeedback, lastFeedback, error, lastError;
    long currentTime, lastTime;
    int integralCumulation, maxCumulation;
    
public:
    PIDController(double p, double i, double d, std::function<T()> pidSource, std::function<void(T)> pidOutput)
        : _p(p), _i(i), _d(d), target(0), output(0), currentFeedback(0), lastFeedback(0), error(0), lastError(0),
          currentTime(0), lastTime(0), integralCumulation(0), maxCumulation(30000) {
        _pidSource.swap(pidSource);
        _pidOutput.swap(pidOutput);
    }

    T tick() {
        currentFeedback = _pidSource();
        
        // Calcul de l'erreur
        error = target - currentFeedback;

        // Calcul de l'intégrale et de la dérivée
        long deltaTime = currentTime - lastTime;
        int cycleIntegral = ((lastError + error) / 2) * deltaTime;
        integralCumulation += cycleIntegral;
        double cycleDerivative = (error - lastError) / deltaTime;

        // Limiter l'intégrale
        if(integralCumulation > maxCumulation) integralCumulation = maxCumulation;
        if(integralCumulation < -maxCumulation) integralCumulation = -maxCumulation;

        // Calcul du résultat PID
        output = (error * _p) + (integralCumulation * _i) + (cycleDerivative * _d);
        
        // Sauvegarder l'état actuel
        lastFeedback = currentFeedback;
        lastError = error;
        lastTime = currentTime;

        // Retourner la valeur du feedback
        _pidOutput(output);
        return currentFeedback;
    }

    void setTarget(T t) { target = t; }
    T getTarget() { return target; }
    T getOutput() { return output; }
    T getFeedback() { return currentFeedback; }
    T getError() { return error; }
};
};

Dans quelle partie du code peut intervenir le PID ?

Module de contrôle des moteurs

Le PID peut être appliqué aux moteurs pour réguler la vitesse et la position des membres du robot.

Exemple : Lorsqu'un membre doit se déplacer, le PID ajuste la puissance envoyée aux moteurs en fonction de l'écart entre la consigne et la position actuelle.

Objectif : Améliorer la fluidité et la précision des mouvements.

Remarque : Nos servomoteurs disposent déjà d'un PID intégré.

Stabilisation du robot

Le PID peut ajuster l'équilibre du robot en analysant les données des capteurs inertiels (IMU) et en corrigeant la posture en temps réel.

Objectif : Minimiser les oscillations et éviter les chutes.

Contrôle de la trajectoire

Lors de la marche, un PID peut corriger les déviations de trajectoire détectées par les capteurs de position.

Objectif : Maintenir une trajectoire stable malgré les irrégularités du sol.

Références

• Sperry, E. (1911). Automatic steering mechanism. U.S. Patent No. 1,000,000.
• Minorsky, N. (1922). Directional stability of automatically steered bodies. Journal of the American Society of Naval Engineers, 34(2), 280-309.
• Åström, K. J., & Hägglund, T. (1995). PID controllers: Theory, design, and tuning (2nd ed.). Instrument Society of America.
• Mosher, N. (2018). PID Controller Implementation in C++. GitHub repository.