Qu'est-ce que le Zero Moment Point (ZMP) ?

---

Le Zero Moment Point (ZMP) est un concept fondamental en robotique humanoïde qui représente le point sur le sol où le moment des forces est nul.

Développé à l'origine pour la marche bipède, le ZMP est utilisé pour évaluer la stabilité d'un robot. Lorsque le ZMP reste à l'intérieur du polygone de sustentation (la zone délimitée par les points de contact avec le sol), le robot maintient son équilibre.

Le savais-tu ?

Le concept de ZMP a été introduit par Miomir Vukobratović dans les années 1960 pour le contrôle des robots marcheurs. Il est aujourd'hui largement utilisé dans les robots humanoïdes comme ASIMO et Atlas.

Principe Général du ZMP

Le ZMP est calculé à partir des forces et moments exercés par le robot sur le sol. Mathématiquement, il peut être exprimé comme :

$$x_{zmp} = \frac{\sum m_i(x_i(\ddot{z}_i + g) - z_i\ddot{x}_i) - \sum I_i\dot{\omega}_{iy}}{\sum m_i(\ddot{z}_i + g)}$$

$$y_{zmp} = \frac{\sum m_i(y_i(\ddot{z}_i + g) - z_i\ddot{y}_i) - \sum I_i\dot{\omega}_{ix}}{\sum m_i(\ddot{z}_i + g)}$$

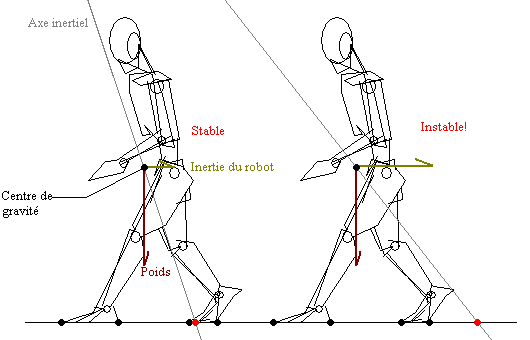
Schéma expliquant le ZMP sur sol horizontal

Source image : Wikipédia - Zero Moment Point

En pratique, le calcul du ZMP nécessite de connaître les positions, accélérations et inerties de tous les segments du robot. Pour les robots équipés de capteurs de force dans les pieds, le ZMP peut également être estimé directement à partir des mesures.

Comment appliquer le ZMP dans un projet robotique ?

Dans un projet de robotique humanoïde ou quadrupède, le ZMP peut être utilisé pour :

• Évaluer la stabilité du robot en temps réel
• Générer des trajectoires de marche stables
• Corriger la posture pour éviter les chutes
• Optimiser la consommation énergétique

class ZMPCalculator:
    def __init__(self, robot_mass, gravity=9.81):
        self.mass = robot_mass
        self.g = gravity
    
    def compute_zmp(self, com_pos, com_acc, total_moment):
        """
        Calcule le ZMP à partir de:
        - com_pos: position du centre de masse (x,y,z)
        - com_acc: accélération du centre de masse (ax,ay,az)
        - total_moment: moment total (Mx, My)
        """
        denominator = self.mass * (com_acc[2] + self.g)
        
        x_zmp = (com_pos[0] * (com_acc[2] + self.g) - 
                com_pos[2] * com_acc[0] - 
                total_moment[1]/self.mass) / denominator
        
        y_zmp = (com_pos[1] * (com_acc[2] + self.g) - 
                com_pos[2] * com_acc[1] + 
                total_moment[0]/self.mass) / denominator
        
        return (x_zmp, y_zmp)

Dans quelle partie du code peut intervenir le ZMP ?

Contrôle de la marche

Le ZMP est essentiel pour générer des trajectoires de marche stables. En surveillant en permanence la position du ZMP, le système de contrôle peut ajuster les mouvements pour maintenir l'équilibre.

Exemple pratique :

Dans un générateur de pas, le ZMP permet de déterminer la position optimale du pied suivant pour garantir la stabilité pendant le transfert de poids.

Objectif : Maintenir le ZMP à l'intérieur du polygone de sustentation pendant au moins 80% du cycle de marche.

Références

• Wikipédia. Zero Moment Point.
• Vukobratović, M., & Borovac, B. (2004). Zero-moment point—Thirty five years of its life. International Journal of Humanoid Robotics, 1(1), 157-173.
• Sardain, P., & Bessonnet, G. (2004). Forces acting on a biped robot. Center of pressure—Zero moment point. IEEE Transactions on Systems, Man, and Cybernetics, 34(5), 630-637.
• Boston Dynamics. Atlas Control System Whitepaper (ZMP-based stabilization).