Qu'est-ce que la Régression Linéaire ?
La Régression Linéaire est l'une des méthodes statistiques les plus fondamentales et les plus utilisées en analyse de données.
La régression linéaire est une méthode statistique qui permet de modéliser la relation entre une variable dépendante (Y) et une ou plusieurs variables indépendantes (X) à l'aide d'une droite. Elle sert à :
- Prédire une valeur : Estimer des résultats futurs basés sur des données historiques
- Comprendre les relations : Quantifier comment une variable influe sur une autre
- Identifier les tendances : Détecter des patterns linéaires dans les données
- Effectuer des analyses : Tester des hypothèses sur les relations entre variables
Le savais-tu ?
La régression linéaire a été développée par Francis Galton au 19ème siècle pour étudier la relation entre les tailles des parents et des enfants. Il a observé que les enfants de parents très grands avaient tendance à être plus petits que leurs parents, et vice versa - un phénomène qu'il a appelé "régression vers la moyenne", donnant ainsi son nom à cette méthode.
Principe Général de la Régression Linéaire
La régression linéaire simple modélise la relation entre deux variables par une droite d'équation :
$$ Y = aX + b + \epsilon $$
Où :
- Y : Variable dépendante
- X : Variable indépendante
- a : Coefficient directeur (pente)
- b : Ordonnée à l'origine
- ε : Terme d'erreur (bruit)
Variable Dépendante : La variable dépendante (Y) est celle que l'on cherche à prédire ou à expliquer. Sa valeur dépend de celle de la variable indépendante. Par exemple, si l'on étudie l'effet de l'entraînement sur la performance, la performance serait la variable dépendante.
Variable Indépendante : La variable indépendante (X) est celle que l'on manipule ou mesure pour observer son influence sur la variable dépendante. Elle est considérée comme la cause dans la relation. Dans l'exemple précédent, l'entraînement serait la variable indépendante.
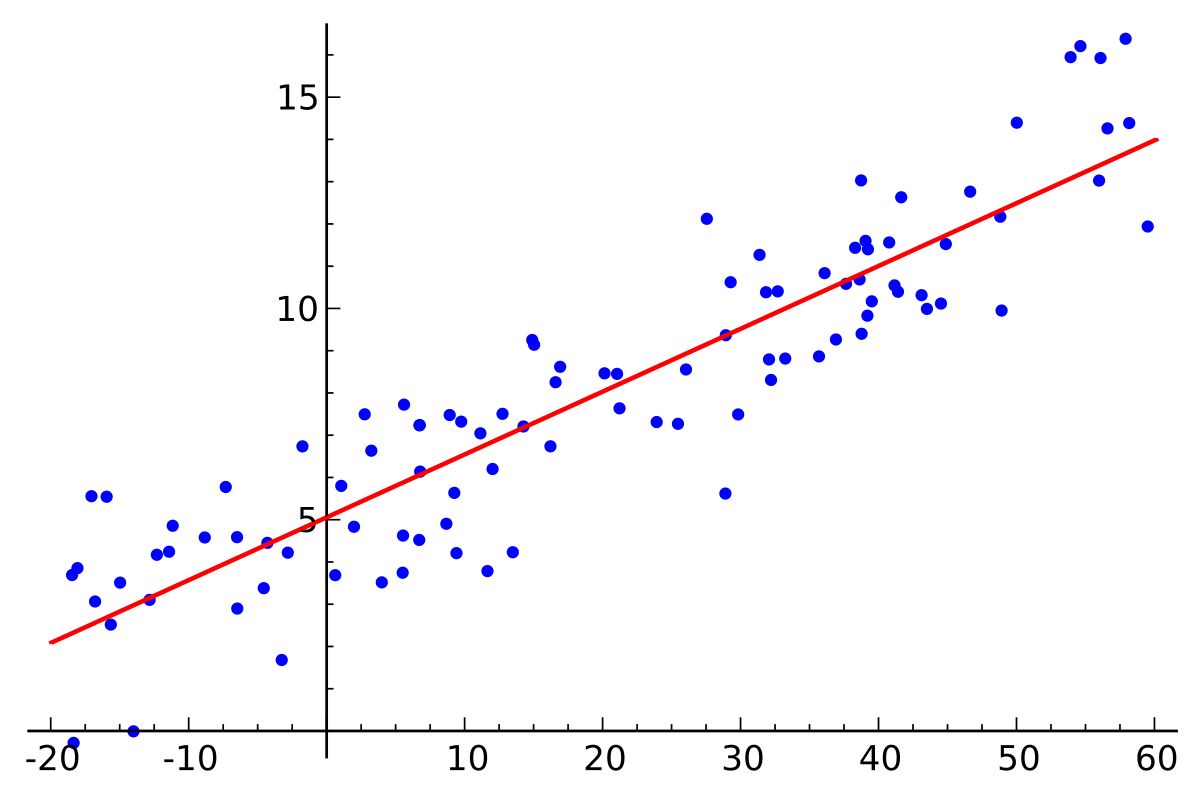
Droite de régression optimale minimisant la somme des carrés des résidus
La méthode des moindres carrés ordinaires (MCO) est utilisée pour trouver les paramètres a et b qui minimisent la somme des carrés des écarts entre les valeurs observées et les valeurs prédites par le modèle.
Cas multivarié
Pour plusieurs variables explicatives, on parle de régression linéaire multiple : $$ Y = a_1X_1 + a_2X_2 + ... + a_nX_n + b + \epsilon $$ Les principes restent similaires, mais l'interprétation devient plus complexe.
Comment appliquer cette notion au projet ?
La régression linéaire peut être utilisée dans divers contextes de projet :
- Prédiction de valeurs futures basées sur des tendances passées
- Analyse de l'impact de différentes variables sur une grandeur mesurée
- Lissage de données bruitées
- Détection d'anomalies (points très éloignés de la droite de régression)
# Exemple avec scikit-learn
import numpy as np
from sklearn.linear_model import LinearRegression
# Données d'exemple
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1) # Variable indépendante
Y = np.array([2, 4, 5, 4, 5]) # Variable dépendante
# Création et entraînement du modèle
model = LinearRegression()
model.fit(X, Y)
# Prédiction
Y_pred = model.predict(X)
# Coefficients
print(f"Coefficient a (pente): {model.coef_[0]:.2f}")
print(f"Ordonnée à l'origine b: {model.intercept_:.2f}")
print(f"Score R²: {model.score(X, Y):.2f}")Dans quels modules peut intervenir la Régression Linéaire ?
Module de stabilisation du robot
La régression peut être utilisée pour analyser l’évolution de l’angle d’inclinaison du robot afin de détecter une perte d’équilibre progressive.
Exemple pratique :
Pendant la marche, on enregistre l’angle d’un gyroscope sur quelques secondes. On ajuste une droite. Si la pente est trop forte (le robot penche trop rapidement), alors une correction moteur peut être déclenchée automatiquement.
Références
- James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning. Springer.
- Montgomery, D. C., Peck, E. A., & Vining, G. G. (2021). Introduction to Linear Regression Analysis. Wiley.
- Pedregosa, F., et al. (2011). Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research.
- Galton, F. (1886). Regression Towards Mediocrity in Hereditary Stature. The Journal of the Anthropological Institute.