Qu'est-ce qu'une Transformée de Fourier ?
La transformée de Fourier est un outil mathématique fondamental permettant de passer d'une vision temporelle à une vision fréquentielle d'un signal. Elle permet de décomposer un signal complexe en une somme d'ondes sinusoïdales simples, facilitant ainsi l'analyse de ses composantes.
Elle est utilisée dans de nombreux domaines : traitement du signal audio, imagerie médicale, analyse vibratoire, robotique, intelligence artificielle, etc.
Le savais-tu ?
Joseph Fourier, physicien français, a introduit cette idée en 1822 dans le but d'étudier la propagation de la chaleur. Aujourd'hui, ses travaux sont essentiels dans l'ingénierie moderne.
Principe Général de la Transformée de Fourier
L'idée principale est que tout signal périodique peut être vu comme une superposition de signaux sinusoïdaux. La transformée de Fourier permet d'identifier ces composantes en déterminant leurs fréquences, amplitudes et phases.
$$F(f) = \int_{-\infty}^{+\infty} x(t) \cdot e^{-j 2\pi f t} \, dt$$
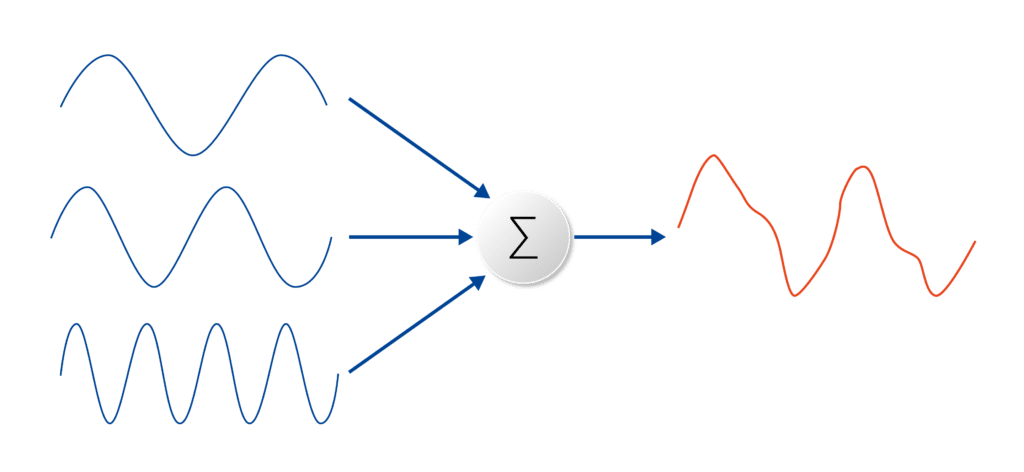
Passage du domaine temporel au domaine fréquentiel
L'équation ci-dessus représente la transformée de Fourier continue. On l'utilise lorsqu'on a un signal analogique. Pour les signaux numériques, on utilise plutôt la transformée de Fourier discrète (TFD), souvent calculée grâce à la FFT (Fast Fourier Transform).
Comment appliquer cette notion au projet ?
Dans le cadre de notre robot bipède, la transformée de Fourier pourrait être utilisée pour analyser les signaux issus des capteurs (IMU, gyroscope, accéléromètre) afin de détecter des oscillations non souhaitées ou pour filtrer les bruits parasites. Cela nous permettrait d'améliorer la stabilité en temps réel via des traitements de signal.
Pour l'implémentation de la transformée de Fourier, je me suis appuyée sur les travaux disponibles en open source, notamment ce code C++ de FFT développé par EE-Abdullah.
template <class T>
#include <Eigen/Dense>
#include <cmath>
#include "../include/FFT.hpp"
int reverse(int b, int n)
{
int k = 1;
int A = b;
int result = 0;
int s = 0;
int A_right = A;
int A_left = A;
while (n-k >= 0)
{
A_right = (int)(A >> n-k) & (int)(std::pow(2, n)-1) & (int)std::pow(2, s);
A_left = (int)(A << n-k) & (int)(std::pow(2, n)-1) & (int)std::pow(2, n-1-s);
result = result | A_left | A_right;
s++;
k += 2;
}
return result;
}
Eigen::VectorXcd order(Eigen::VectorXd& x_n)
{
int N = x_n.size();
int n_bits = std::log2(N);
Eigen::VectorXcd x_n_ord(N);
int new_index = 0;
for (int i=0; i<N; ++i)
{
new_index = reverse(i, n_bits);
x_n_ord(i) = x_n(new_index);
}
return x_n_ord;
}
Eigen::VectorXcd computation(Eigen::VectorXcd&& x_seg_A, Eigen::VectorXcd&& x_seg_B, int N)
{
int N_prev = x_seg_A.size();
int N_next = N_prev * 2;
int s = (int)std::log2(N_next);
int W_length = std::pow(2, s-1);
std::complex<double> W = std::polar(1.0, -2*M_PI/N);
Eigen::VectorXcd W_K(W_length);
int num_pairs = (int)(N/(std::pow(2, s)));
W_K.setConstant(W);
W_K = W_K.binaryExpr(
Eigen::VectorXcd::LinSpaced(W_K.size(), 0, W_K.size()-1),
[&](std::complex<double> w_k, std::complex<double> i) {
return std::pow(w_k, num_pairs*i.real());
}
);
Eigen::VectorXcd H_K = W_K.cwiseProduct(x_seg_B);
Eigen::VectorXcd X_K(N_next);
X_K.segment(0, W_length) = x_seg_A + H_K;
X_K.segment(W_length, W_length) = x_seg_A - H_K;
return X_K;
}
Eigen::VectorXcd segment(Eigen::VectorXcd& x_n_sort)
{
int N = x_n_sort.size();
int total_stages = (int)std::log2(N);
Eigen::VectorXcd X_K = x_n_sort;
int num_pairs = 0;
int index = 0;
int input_chunk = 0;
int output_chunk = 0;
for (int s=1; s<=total_stages; ++s) {
index = 0;
input_chunk = (int)(std::pow(2, s-1));
output_chunk = (int)(std::pow(2, s));
num_pairs = (int)(N/(std::pow(2, s)));
for (int i=1; i<=num_pairs; ++i) {
X_K.segment(index, output_chunk) =
computation(
X_K.segment(index, input_chunk),
X_K.segment(index+input_chunk, input_chunk),
N
);
index = index + output_chunk;
}
}
return X_K;
}
Eigen::VectorXcd FFT(Eigen::VectorXd& x_n)
{
int N = x_n.size();
Eigen::VectorXcd x_n_ord = order(x_n);
Eigen::VectorXcd X_K = segment(x_n_ord);
return X_K;
}Dans quelle partie du code peut intervenir la Transformée de Fourier ?
Acquisition des données
La FFT peut être utilisée pour analyser les données des capteurs inertiels et détecter des vibrations ou oscillations indésirables.
Exemple pratique :
Lors de l'acquisition des données, le capteur IMU envoie des mesures d'accélération et de vitesse angulaire sur plusieurs axes (X, Y, Z). Ces signaux sont ensuite échantillonnés à des intervalles réguliers. En appliquant la FFT sur les données temporelles, on obtient un spectre de fréquence qui nous permet d'identifier les pics de fréquence. Par exemple, si un pic se trouve à une fréquence de 50 Hz, cela peut indiquer une vibration indésirable provenant d’un moteur ou d'un autre composant du robot.Une fois identifiées, ces fréquences peuvent être filtrées ou atténuées à l’aide de filtres passe-bas ou passe-bande pour minimiser leur impact sur les performances du robot.
Références
- Fourier, J. (1822). Théorie analytique de la chaleur. Firmin Didot.
- Cooley, J. W., & Tukey, J. W. (1965). An algorithm for the machine calculation of complex Fourier series. Mathematics of Computation.
- Abdullah, E. E. (2020). FFT Implementation in C++. GitHub repository.
- Smith, S. W. (1997). The Scientist and Engineer's Guide to Digital Signal Processing. California Technical Publishing.